
MATEMÁTICA
PARA CHICOS DE PRIMER GRADO DE PRIMARIA

Cartas que dan diez
Te proponemos:
Una versión rápida del tradicional juego de “la casita robada”. Para hacer la actividad más divertida podemos invitar a un miembro de nuestra familia a jugar, se puede jugar en forma individual o en parejas de a dos integrantes.
Materiales:
- Un mazo de cartas con los números del uno al nueve.
Reglas del juego:
1. Se reparten 3 cartas a cada equipo. Hay que colocar también, antes de iniciar, 4 cartas (boca arriba) sobre la mesa.
2. Por turnos, las parejas deben analizar si pueden formar la suma de 10 usando una de las cartas que tienen en la mano junto a otra que esté en la mesa. De ser posible, los jugadores de ese equipo se llevan ambas cartas a su baraja.
3. Si no se logró sumar 10 en esa ronda, hay que dejar una de nuestras cartas.
4. Hay que estar atentos. Cuando un equipo tira una carta y no advierte que es capaz de llegar al número 10, la otra pareja puede “soplar” esas cartas y llevárselas.
5. Al finalizar el mazo, gana la pareja que tiene más cartas en su pozo.
Actividad extra:
Magdalena tiene una carta con el número 7 y, en el centro de la mesa, la baraja muestra los dígitos 3, 6 y 4.
1. Elige la carta con la que ella puede obtener la suma de 10. Explica cómo pensaste el resultado y no te olvides de registrar en un cuaderno los procedimientos.
PARA ALUMNOS DE SEGUNDO GRADO DE PRIMARIA
Código secreto
En esta propuesta:
Vamos a convertirnos en detectives o buscadores de fortuna al intentar descifrar algunas contraseñas con números. Podés participar solo para aumentar el desafío o buscar la ayuda de un adulto.
Primera parte:
En este juego, para poder encontrar grandes tesoros hay que abrir puertas ocultas. Estas tienen escritos números y códigos secretos que debemos descifrar. Al observarlas, las puertas están formadas por dos ladrillos que pueden estar ubicados de las siguientes maneras:

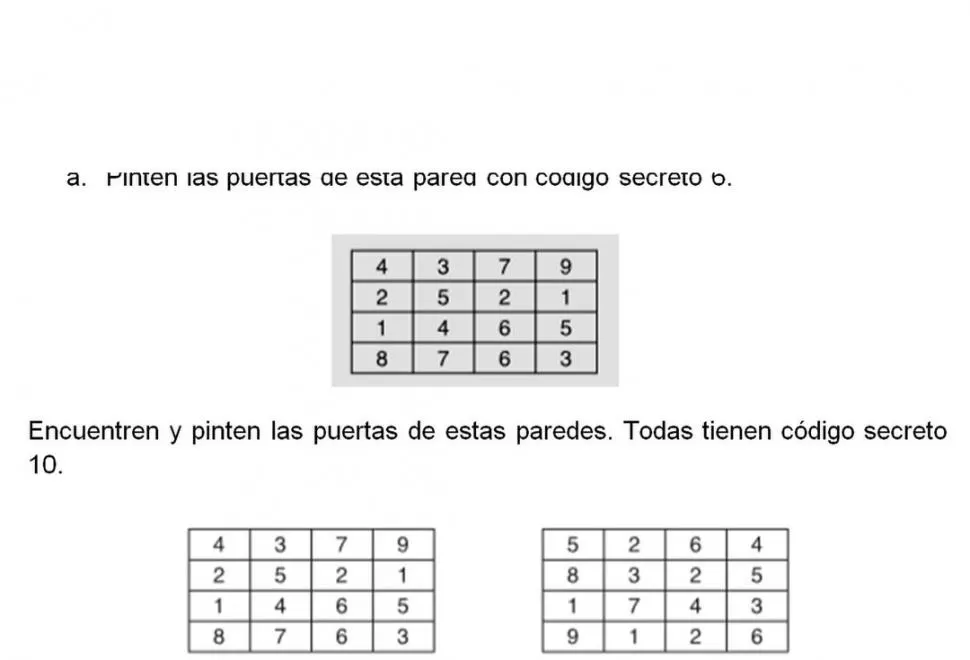
Por ejemplo, si en una pared el código secreto es 6, para encontrar la respuesta misteriosa hay que buscar dos ladrillos que juntos sumen 6.
Procedimiento:
1. Localizá en esta pared las puertas que tengan como código secreto un 6.
2. Para no confundirte, podés pintar o marcar con un lápiz los resultados.
3. Responde: ¿cuáles pueden ser las combinaciones de números que aparecen en los dos ladrillos para que el código secreto sea 9? Escribe todas las respuestas posibilidades.
Segunda parte:
Procedimiento:
1. Encuentra y remarca las puertas de estas paredes. Ambas tienen como código secreto al número 10.
Tercera parte:
Procedimiento:
1. Crea dos paredes con números y escribeles un dígito de acceso secreto. Pedile a un familiar que participe e intente descifrarlo.
2. Responde: Nicolás dice que, sin hacer las sumas de todos los ladrillos, con los que tiene alrededor se da cuenta rápidamente de cuáles son las puertas que tienen el código secreto. ¿Cómo crees que lo resuelve? Anota tus ideas en un cuaderno.
Para reflexionar:
¿Cuántas sumas distintas, de dos sumandos cada una, pueden escribirse para obtener códigos entre el uno y el nueve? Para averiguarlo, una pequeña ayuda es organizar las sumas en tablas o separarlas entre sí. Por ejemplo: las sumas que empiezan con cero pueden ir en una hoja, las que comienzan con 1 en otra y así sucesivamente.
PARA CHICOS DE TERCER GRADO DE PRIMARIA
Competencias
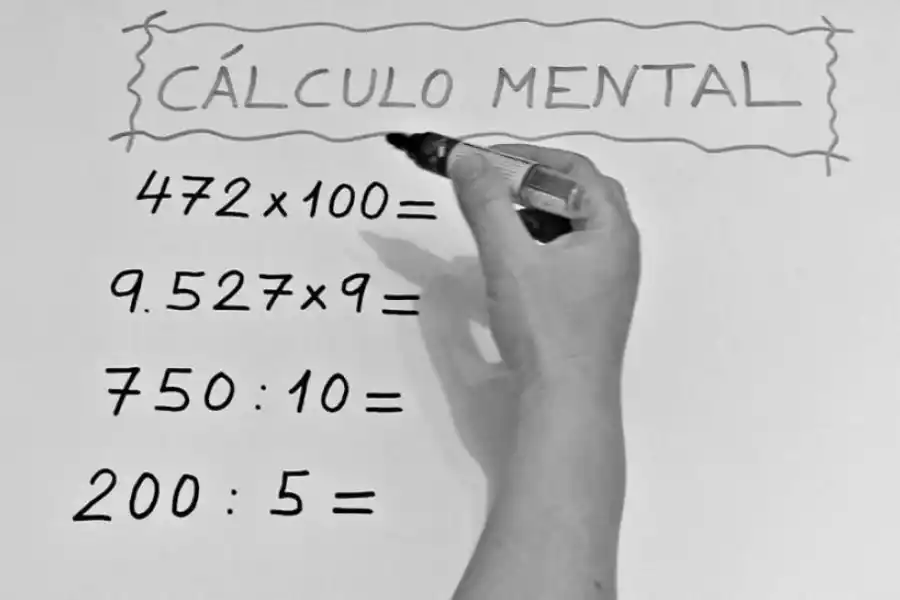
Te proponemos:
Potenciar y practicar las sumas de los números para poder hacer algunos calculos mentales. Al necesitar ayuda o corroborar los datos no dudes en pedirle a un familiar que chequee la información obtenida.
Primer ejercicio:
Procedimiento:
Imagina que en el monitor de tu computadora aparecen 3 dígitos distintos. Para ganar, hay que armar todos los números de 2 cifras distintas que se pueda y ordenarlos en escalera de menor a mayor.
Preguntas:
1. Si vieras los dígitos 8, 5 y 3 ¿qué números se formarían? ¿Cuál es la escalera que deberías trazar para organizarlos?
2. Ahora es tu turno de escribir 3 cifras distintas y armar las escaleras que resulten posibles. ¿Cuántos números tiene cada una de las escaleras que armaste? ¿Estás seguro de que no puede tener más? Justifica las respuestas en un cuaderno.
Segundo ejercicio:
Preguntas:
1. Marcos dice que, cuando aparecen los números 4, 5 y 8, logra escribir 6 números. Luego, al ver los dígitos 6, 7 y 9, afirma que escribirá más combinaciones porque estos números son mayores. ¿Te parece que Marcos tiene razón? Explica el resultado.
2. Si hubiera que construir números de a tres, ¿la cantidad de números formados sería la misma?
3. Ahora en la pantalla de la PC aparecen 4 dígitos para armar números de 3 cifras distintas: 3, 5, 6, 8. ¿Cuántos números es posible armar?
Tercer ejercicio:
Juan Pablo hace árboles para ordenar los números. Si quiere armar números de 2 cifras con 4, 8, 9 y ordenarlos, él hace así:
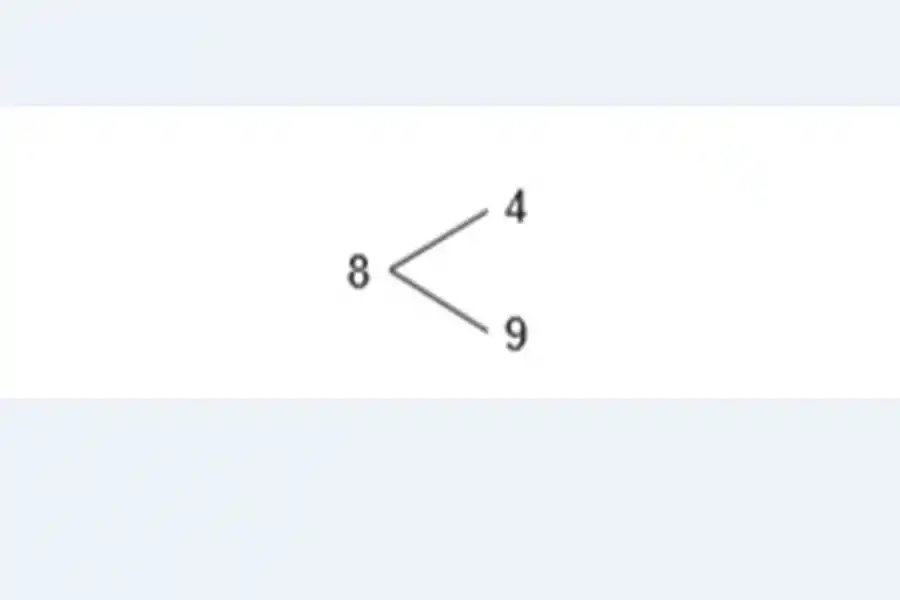
Y obtiene los números: 48; 49; 84; 89; 94; 98. Usa la estrategia de Juan Pablo para controlar los resultados que encontraste en los problemas matemáticos anteriores.













